|
I am a PhD student in machine learning at MIT, where I am fortunate to be advised by Ankur Moitra. I am also a member of the wonderful Atomic Architects, led by Tess Smidt. Previously, I was a summer research intern at DE Shaw Research, working on tokenization of small molecules for LLMs, and at the Open Catalyst Team at Meta FAIR, studying equivariant architecture for chemistry applications. Before graduate school, I was a research analyst at the Center for Computational Mathematics of the Flatiron Institute in New York, where I worked on developing algorithms at the interface of equivariant deep learning and signal processing for cryoEM. Broadly, I enjoy developing theoretically principled tools for deep learning (often in scientific domains), with a focus on both understanding and imposing structure for neural representations. I spent summer 2019 at Microsoft Research, where I was lucky to be mentored by Cameron Musco. I've also spent productive summers at Reservoir Labs and the Center for Computational Biology. I was an undergrad at Yale in applied math and computer science, where I had the good fortune of being advised by Amin Karbasi and Dan Spielman. Finally, I co-founded the Boston Symmetry Group, which hosts a recurring workshop for researchers interested in symmetries in machine learning. Follow us on Twitter, shoot us an email, or join our mailing list if you're interested in attending! Email / Github / LinkedIn / Twitter / Google Scholar |

|
|
My primary research interests include symmetry-aware (equivariant) machine learning and scientific applications. In addition, I enjoy developing theoretically principled tools for deep learning, for applications from vision to interpretability to PDEs.
|
|
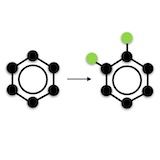
Hannah Lawrence*, Vasco Portilheiro*, Yan Zhang, Sékou-Oumar Kaba, ICML, 2024. Equivariant models can't break symmetries - they can only map symmetric inputs (e.g. squares) to symmetric outputs (e.g. objects with the same symmetry as a square). We propose a sample-efficient probabilistic framework for breaking symmetries, e.g. in generative models' latent spaces, by combining equivariant networks with canonicalization-based positional encodings. |
 
|
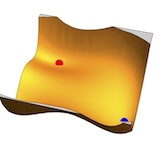
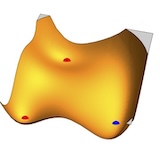
Nadav Dym*, Hannah Lawrence*, Jonathan Siegel* ICML, 2024. We demonstrate that, perhaps surprisingly, there is no continuous canonicalization (or even efficiently implementable frame) for many symmetry groups. We introduce a notion of weighted frames to circumvent this issue. |
|
Hannah Lawrence*, Mitchell Harris* ICLR, 2024. We propose machine learning approaches, which are equivariant with respect to the non-compact group of area-preserving transformations SL(2,R), for learning to solve polynomial optimization problems. |
 
|
Bobak T. Kiani*, Thien Le*, Hannah Lawrence*, Stefanie Jegelka, Melanie Weber ICLR, 2024. We give statistical query lower bounds for learning symmetry-preserving neural networks and other invariant functions. |
|
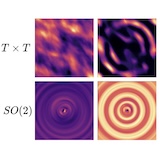
Derek Lim*, Hannah Lawrence, Ningyuan (Teresa) Huang, Erik H. Thiede ICML TAG-ML Workshop, 2023. We observe that many popular positional encodings (sinusoidal, ROPE, graph PEs, etc) can be interpreted as algebraic group representations, which formalizes some of their desirable properties (invariance to global translation, etc). This also suggests a simple framework for building positional encodings with new invariances, such as the special euclidean group. |
|
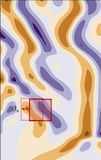
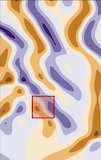
Grégoire Mialon*, Quentin Garrido*, Hannah Lawrence, Danyal Rehman, Bobak Kiani ICLR, 2023. We apply self-supervised learning to partial differential equations, using the equations' Lie point symmetries as augmentations. |
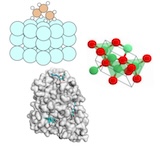 
|
Xuan Zhang*, Limei Wang*, Jacob Helwig*, Youzhi Luo*, Cong Fu*, Yaochen Xie*, ..., Hannah Lawrence, ..., Shuiwang Ji Under review, 2023. A survey of machine learning for physics. |
|
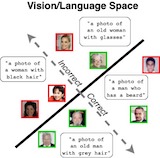
Saachi Jain*, Hannah Lawrence*, Ankur Moitra, Aleksander Madry ICLR (spotlight presentation), 2023. See also the blog post We present a framework for automatically identifying and captioning coherent patterns of errors made by any trained model. The key? Keeping it simple: linear classifiers in a shared vision-language embedding space. |
|
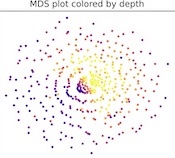
Enric Boix-Adsera, Hannah Lawrence, George Stepaniants, Philippe Rigollet NeurIPS (Oral Presentation), 2022 We define a family of distance pseudometrics for comparing learned data representations, directly inspired by transfer learning. In particular, we define a distance between two representations based on how differently (worst-case over all downstream, bounded linear predictive tasks) they perform under ridge regression. |
|
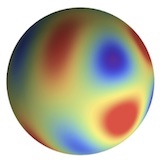
Hannah Lawrence NeurIPS Workshop: Symmetry and Geometry in Neural Representations (Poster, to appear), 2022 We extend Barron’s Theorem for efficient approximation to invariant neural networks, in the cases of invariance to a permutation subgroup or the rotation group. |
 
|
Michael Kapralov, Hannah Lawrence, Mikhail Makarov, Cameron Musco, Kshiteej Sheth Symposium on Discrete Algorithms (SODA), to appear, 2023 We prove that any nearly low-rank Toeplitz positive semidefinite matrix has a low-rank approximation that is itself Toeplitz, and give a sublinear query complexity algorithm for finding it. |
|
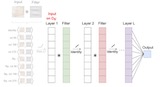
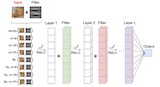
Hannah Lawrence, Kristian Georgiev, Andrew Dienes, Bobak T. Kiani* Appearing at ICML, 2022 We characterize the implicit bias of linear group-convolutional networks trained by gradient descent. In particular, we show that the learned linear function is biased towards low-rank matrices in Fourier space. |
|
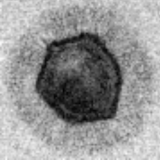
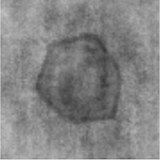
Hannah Lawrence * , David A. Barmherzig *, Henry Li, Michael Eickenberg, Marylou Gabrié Appeared at MSML, 2021 By using a maximum-likelihood objective coupled with a deep decoder prior for images, we achieve superior image reconstruction for holographic phase retrieval, including under several challenging realistic conditions. To our knowledge, this is the first dataset-free machine learning approach for holographic phase retrieval. |
|
Lin Chen, Qian Yu, Hannah Lawrence, Amin Karbasi Appeared at NeurIPS, 2020 We establish the minimax regret of switching-constrained online convex optimization, a realistic optimization framework where algorithms must act in real-time to minimize cumulative loss, but are penalized if they are too erratic. |
 
|
Hannah Lawrence, Jerry Li, Cameron Musco, Christopher Musco Appeared at ICASSP, 2020 By building new, randomized "ruler" sampling constructions, we show how to use sublinear sparse Fourier transform algorithms for sample efficient, low-rank, Toeplitz covariance estimation. |
|
|
 |
Organizer, Boston Symmetry Day, Fall 2023 - Present
Teaching Assistant, 6.S966 Symmetry and its Applications to Machine Learning, Spring 2023 Hertz Foundation Summer Workshop Committee, Fall 2021 and Spring 2022 Women in Learning Theory Mentor, Spring 2020 Applied Math Departmental Student Advisory Committee, Spring 2019 Dean's Committee on Science and Quantitative Reasoning, Fall 2018 Undergraduate Learning Assistant, CS 365 (Design and Analysis of Algorithms), Spring 2018 Undergraduate Learning Assistant, CS 223 (Data Structures and Algorithms), Spring 2017 Undergraduate Learning Assistant, CS 201 (Introduction to Computer Science), Fall 2017 |
|
|